Showing posts with label Story. Show all posts
Showing posts with label Story. Show all posts
Wednesday, September 1, 2010
Tuesday, August 31, 2010
Concept: Third Draft
This is a simplified model of the first draft, the permutations and combinations of which allow children to animate characters, perform actions, modify them. and therefore explore the mathematics involved.
THE 5 BLOCKS:
People, Animals (Characters)
The player starts with choosing a person/animal/both. Each cube has 5 working sides, each representing a different person/animal.

Actions (For characters)
These can be used to give the character properties- Eg. Jump, Run, Dance etc.
Modifiers (For actions)
These are tools that are applied to actions, to increase/decrease the rate/time etc mathematically.
Comparisons (For characters)
These are tools that can be used to compare sizes/weights of different characters.
THE MODEL:
CATEGORIES:
HOW TO USE:
Pick your character/s:
Start by picking a person or/and animal.
Character properties: Name, Age, Weight and Height, Description.
Comparisons:
Compare the size/weight/height of characters. You can see these comparisons in different representations, eg. percentages, fractions, etc. therefore learning about the relationship between different mathematical tools.
Actions:
Animate your character by using the ‘Action’ block. When the action is placed next to the character, the character is performs the corresponding action. If the action block is placed BETWEEN two characters, both characters perform the same action (Diagram 2). If it is placed near one, only that one is performs the action (Diagram 3).
Modifiers:
Modify your actions by adding the ‘Modifier’ block. Watch your character perform the action at a faster/slower rate, calculate the time taken, the distance traversed etc.
KEY ELEMENTS:
Characterization and Humour
EXAMPLES OF NARRATIVES:
Make your own problem:
Make a man run, check the distance covered.
Then make a mouse run at the same speed, and check the distance covered. What is the difference? Why? Then double the speed of the mouse and see the difference. Try the same with an elephant.
Humourous situations:
Make a man jump, add a mouse to the scene, and then double the speed of the man!
Then make the man run away from the mouse, and draw the mouse running at triple the speed of the man!
Random:
Make a baby dance, in slow motion. Then make him squat, and increase the speed. Then try making the horse dance with the baby!
THE 5 BLOCKS:
People, Animals (Characters)
The player starts with choosing a person/animal/both. Each cube has 5 working sides, each representing a different person/animal.

Actions (For characters)
These can be used to give the character properties- Eg. Jump, Run, Dance etc.
Modifiers (For actions)
These are tools that are applied to actions, to increase/decrease the rate/time etc mathematically.
Comparisons (For characters)
These are tools that can be used to compare sizes/weights of different characters.
THE MODEL:
CATEGORIES:
HOW TO USE:
Pick your character/s:
Start by picking a person or/and animal.
Character properties: Name, Age, Weight and Height, Description.
Comparisons:
Compare the size/weight/height of characters. You can see these comparisons in different representations, eg. percentages, fractions, etc. therefore learning about the relationship between different mathematical tools.
Actions:
Animate your character by using the ‘Action’ block. When the action is placed next to the character, the character is performs the corresponding action. If the action block is placed BETWEEN two characters, both characters perform the same action (Diagram 2). If it is placed near one, only that one is performs the action (Diagram 3).
Modifiers:
Modify your actions by adding the ‘Modifier’ block. Watch your character perform the action at a faster/slower rate, calculate the time taken, the distance traversed etc.
KEY ELEMENTS:
Characterization and Humour
EXAMPLES OF NARRATIVES:
Make your own problem:
Make a man run, check the distance covered.
Then make a mouse run at the same speed, and check the distance covered. What is the difference? Why? Then double the speed of the mouse and see the difference. Try the same with an elephant.
Humourous situations:
Make a man jump, add a mouse to the scene, and then double the speed of the man!
Then make the man run away from the mouse, and draw the mouse running at triple the speed of the man!
Random:
Make a baby dance, in slow motion. Then make him squat, and increase the speed. Then try making the horse dance with the baby!
Monday, August 30, 2010
Simplify
Figuring out the system and interactions:
To make it easier to understand how the model works, I started exploring the permutations and combinations with building blocks. I realized that the system is still quite complicated, and including different scenarios and situations which interact with each other would be too difficult to interact with, as well as program.
Meeting with Victor:
Adding stories within the tool is not necessary- Let the child explore and play with the options and create their own narrative.
In the current system, there are fixed options within the scenario, which diverts from the main focus of “mathematics”-Too complex (to understand, interact with, and program)
SIMPLIFY- There can be many options with just 3-4 blocks, and is easier for a child to understand/play with.
To make it easier to understand how the model works, I started exploring the permutations and combinations with building blocks. I realized that the system is still quite complicated, and including different scenarios and situations which interact with each other would be too difficult to interact with, as well as program.
Meeting with Victor:
Adding stories within the tool is not necessary- Let the child explore and play with the options and create their own narrative.
In the current system, there are fixed options within the scenario, which diverts from the main focus of “mathematics”-Too complex (to understand, interact with, and program)
SIMPLIFY- There can be many options with just 3-4 blocks, and is easier for a child to understand/play with.
Sunday, August 29, 2010
Friday, August 27, 2010
Concept: Second Draft
Loopholes in the first draft:
After speaking to some people about my earlier concept, I realized that it was a little clinical in its approach- Unless a child was motivated enough, with a high interest in mathematics, he wouldn't want to explore the possibilites of the blocks. I needed to make the interface more user friendly and fun- something that a child would be interested in playing with, and therefore engaging with mathematics. This version focusses more on situations, characters and storytelling, still maintaining the interactivity and exploratory aspect of the earlier version.
Rethinking the concept:
Making an interactive mathematical narrative; building your own story with the help of scenarios. All interactions and scenarios focus on the application of math in everyday situations.
There are four types of building blocks- You (Character), Travel, People (This includes 3 blocks of real world people and scenarios that can be interacted with) and Places (3 blocks of places where children can learn about the application of math). Each face of each block corresponds to a different property of that person/scenario. (For example, the “Travel” block, will have an auto, car, train and bus on the faces of the block respectively)
You begin by choosing a character, and this character then interacts with different people/places/transport mathematically by arranging the cubes (with respective faces) in any order- Like building a storyboard.
Children can use this device to build their own stories, engage with mathematics, and relate it to the real world.
Mediums and Technology:
Stop motion/Basic animation
Motion graphics
Augmented reality
Projection mapping
Multi touch screen
After speaking to some people about my earlier concept, I realized that it was a little clinical in its approach- Unless a child was motivated enough, with a high interest in mathematics, he wouldn't want to explore the possibilites of the blocks. I needed to make the interface more user friendly and fun- something that a child would be interested in playing with, and therefore engaging with mathematics. This version focusses more on situations, characters and storytelling, still maintaining the interactivity and exploratory aspect of the earlier version.
Rethinking the concept:
Making an interactive mathematical narrative; building your own story with the help of scenarios. All interactions and scenarios focus on the application of math in everyday situations.
There are four types of building blocks- You (Character), Travel, People (This includes 3 blocks of real world people and scenarios that can be interacted with) and Places (3 blocks of places where children can learn about the application of math). Each face of each block corresponds to a different property of that person/scenario. (For example, the “Travel” block, will have an auto, car, train and bus on the faces of the block respectively)
You begin by choosing a character, and this character then interacts with different people/places/transport mathematically by arranging the cubes (with respective faces) in any order- Like building a storyboard.
Children can use this device to build their own stories, engage with mathematics, and relate it to the real world.
Mediums and Technology:
Stop motion/Basic animation
Motion graphics
Augmented reality
Projection mapping
Multi touch screen
Saturday, August 21, 2010
Rethinking structure
Categories (In progress):
Examples of permutations (Scenarios):
Narrative options:
- Is it a learning tool? A toy? Or a game? Or all?
- Make your own problem: Setting the scene for them to create their own problem.
- Goal: Single Goal/Multiple goals
- Nudge
- Reward or threat-Clues
- Travel- Journey- Destination
- Competition: Permutations/combinations to reach the respective place fastest
- Fastest way to get somewhere
- Narrative in parts: Level one/Level two
- Building characters, building landscapes/scenarios
- Have a fixed amount of money through a place- Simulated
- Each step requires the child to calculate in order to progress
- Understanding daily situations in the context of mathematics
- Demonstrating a concept directly vs implied
Saturday, August 7, 2010
Siftables- The toy blocks that think
Toys that inspire learning, innovation — and of course fun! These are the toys of the technological age: they are alive, they think, they perform magic. What were your favorite toys as a kid (or an adult), and what did they inspire in you? David Merrill replaces traditional building blocks with electronic tiles that can add, subtract, compose and create.
Siftables aims to enable people to interact with information and media in physical, natural ways that approach interactions with physical objects in our everyday lives. As an interaction platform, Siftables applies technology and methodology from wireless sensor networks to tangible user interfaces. Siftables are independent, compact devices with sensing, graphical display, and wireless communication capabilities. They can be physically manipulated as a group to interact with digital information and media. Siftables can be used to implement any number of gestural interaction languages and HCI applications.
More about siftables:
http://sifteo.com/
http://alumni.media.mit.edu/~dmerrill/siftables.html
http://tacolab.com/projects/Siftables
Siftables aims to enable people to interact with information and media in physical, natural ways that approach interactions with physical objects in our everyday lives. As an interaction platform, Siftables applies technology and methodology from wireless sensor networks to tangible user interfaces. Siftables are independent, compact devices with sensing, graphical display, and wireless communication capabilities. They can be physically manipulated as a group to interact with digital information and media. Siftables can be used to implement any number of gestural interaction languages and HCI applications.
More about siftables:
http://sifteo.com/
http://alumni.media.mit.edu/~dmerrill/siftables.html
http://tacolab.com/projects/Siftables
Thursday, August 5, 2010
Maths Mela (By Prithvi Theatre, Mumbai)
At Avalon Heights International School, August 2nd and 3rd:
The students of the school conducted the maths workshop, where there were different games based on mathematical concepts. Students from different schools visited the workshop in batches. The concepts that the mela focussed on were not direct applications of the curriculum, but more about mathematical “wonders”.
Unfortunately, photography was prohibited at the mela. These are some of the concepts that the exhibits were based on:
The Seven Bridges of Konigsberg
The Seven Bridges of Konigsberg is a notable historical problem in mathematics. Its negative resolution by Leonhard Euler in 1735 laid the foundations of graph theory and presaged the idea of topology. The problem was to find a walk through the city that would cross each bridge once and only once. The islands could not be reached by any route other than the bridges, and every bridge must have been crossed completely every time (one could not walk half way onto the bridge and then turn around and later cross the other half from the other side). Euler proved that the problem has no solution.
At the mela, there was a 3d model of this problem, and students were trying to make a toy car travel through as many bridges as possible. The concept was then explained to them.
MathMagic
Pick a number between 1 and 60. There are five boards with random numbers in a grid. The “magician” will guess the number on your mind by checking if it appears on any of the boards. The number on your mind is the sum of the first numbers on all the boards that your number appears on.
Ames Room
An Ames room is a distorted room that is used to create an optical illusion. An Ames room is constructed so that from the front it appears to be an ordinary cubic-shaped room, with a back wall and two side walls parallel to each other and perpendicular to the horizontally level floor and ceiling. However, this is a trick of perspective and the true shape of the room is trapezoidal. As a result of the optical illusion, a person standing in one corner appears to the observer to be a giant, while a person standing in the other corner appears to be a dwarf. The illusion is convincing enough that a person walking back and forth from the left corner to the right corner appears to grow or shrink. This is used in television, special effects, etc.
At the mela, there was a 3D exhibit which children could learn this phenomen from. Through a peephole, they could see the optical illusion created.
Elliptical Carrom Board
With the striker and the other coin at the two focus points of the ellipse, when the striker is hit at any point of the circumference of the ellipse, it definitely passes through the second focus point, that is, hits the other coin.
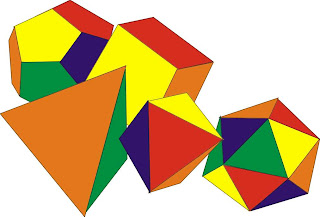
The 5 platonic solids
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and angles.
There are precisely five Platonic solids: Cube, Tetrahedron, Octahedron, Dodecahedron and Icosahedron
Playing with geometry, Constructions
Children played with straws, flat shapes, and blocks and built sculptures.
3D Animation
The origin of numbers, the 0, 1, the concept of binary numbers, the Fibonacci numbers, and the abacus.
The students of the school conducted the maths workshop, where there were different games based on mathematical concepts. Students from different schools visited the workshop in batches. The concepts that the mela focussed on were not direct applications of the curriculum, but more about mathematical “wonders”.
Unfortunately, photography was prohibited at the mela. These are some of the concepts that the exhibits were based on:
The Seven Bridges of Konigsberg
The Seven Bridges of Konigsberg is a notable historical problem in mathematics. Its negative resolution by Leonhard Euler in 1735 laid the foundations of graph theory and presaged the idea of topology. The problem was to find a walk through the city that would cross each bridge once and only once. The islands could not be reached by any route other than the bridges, and every bridge must have been crossed completely every time (one could not walk half way onto the bridge and then turn around and later cross the other half from the other side). Euler proved that the problem has no solution.
At the mela, there was a 3d model of this problem, and students were trying to make a toy car travel through as many bridges as possible. The concept was then explained to them.
MathMagic
Pick a number between 1 and 60. There are five boards with random numbers in a grid. The “magician” will guess the number on your mind by checking if it appears on any of the boards. The number on your mind is the sum of the first numbers on all the boards that your number appears on.
Ames Room
An Ames room is a distorted room that is used to create an optical illusion. An Ames room is constructed so that from the front it appears to be an ordinary cubic-shaped room, with a back wall and two side walls parallel to each other and perpendicular to the horizontally level floor and ceiling. However, this is a trick of perspective and the true shape of the room is trapezoidal. As a result of the optical illusion, a person standing in one corner appears to the observer to be a giant, while a person standing in the other corner appears to be a dwarf. The illusion is convincing enough that a person walking back and forth from the left corner to the right corner appears to grow or shrink. This is used in television, special effects, etc.
At the mela, there was a 3D exhibit which children could learn this phenomen from. Through a peephole, they could see the optical illusion created.
Elliptical Carrom Board
With the striker and the other coin at the two focus points of the ellipse, when the striker is hit at any point of the circumference of the ellipse, it definitely passes through the second focus point, that is, hits the other coin.
The 5 platonic solids
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and angles.
There are precisely five Platonic solids: Cube, Tetrahedron, Octahedron, Dodecahedron and Icosahedron
Playing with geometry, Constructions
Children played with straws, flat shapes, and blocks and built sculptures.
3D Animation
The origin of numbers, the 0, 1, the concept of binary numbers, the Fibonacci numbers, and the abacus.
Friday, July 23, 2010
Flatland
Flatland: A Romance of Many Dimensions is a satirical novella by the English schoolmaster Edwin Abbott Abbott. Writing pseudonymously as "a square", Abbott uses the fictional two-dimensional world of Flatland to offer pointed observations on the social hierarchy of Victorian culture. However, the novella's more enduring contribution is its examination of dimensions. Noted science writer Isaac Asimov described Flatland as "The best introduction one can find into the manner of perceiving dimensions."
(The story is about a two-dimensional world referred to as Flatland which is occupied by geometric figures, line-segments (females) and regular polygons with various numbers of sides.The narrator is a humble Square, a member of the social caste of gentlemen and professionals in a society of geometric figures, who guides us through some of the implications of life in two dimensions.The narrator is then visited by a three-dimensional sphere, which he cannot comprehend until he sees Spaceland for himself.After the Square's mind is opened to new dimensions, he tries to convince the Sphere of the theoretical possibility of the existence of a fourth (and fifth, and sixth ...) spatial dimension.)
Wednesday, July 21, 2010
Role-Playing Your Way to Math Mastery?
A massively multiplayer online game requiring players to employ mathematical concepts could revolutionize the teaching of mathematics at the middle school level, according to Stanford mathematician Keith Devlin.
Key points:
-The importance of 'context'
-Using mathematics to achieve goals, and to see the outcome of that immediately
-Video games help students overcome that period when they haven’t seen value in the mathematics they learn
-The one thing that is missing in a math class is the meaningful environment
Tuesday, July 20, 2010
Children's Number books at the M.A.I.S Junior Library
Observations:
Simple narrative style
Questioning and Problem solving through storytelling
Colourful and friendly illustrations
Basic interactivity (Counting beads)
Bold use of type
Simple narrative style
Questioning and Problem solving through storytelling
Colourful and friendly illustrations
Basic interactivity (Counting beads)
Bold use of type
Ko's Journey: An online story-based math adventure
Ko's Journey is a first of its kind web-based application designed to teach the core concepts of middle school math through storytelling. Paced for learning and comprehension, it provides more depth and context than most math games.
http://www.kosjourney.com
http://imagineeducation.org
Subscribe to:
Posts (Atom)