At Avalon Heights International School, August 2nd and 3rd:
The students of the school conducted the maths workshop, where there were different games based on mathematical concepts. Students from different schools visited the workshop in batches. The concepts that the mela focussed on were not direct applications of the curriculum, but more about mathematical “wonders”.
Unfortunately, photography was prohibited at the mela. These are some of the concepts that the exhibits were based on:
The Seven Bridges of Konigsberg
The Seven Bridges of Konigsberg is a notable historical problem in mathematics. Its negative resolution by Leonhard Euler in 1735 laid the foundations of graph theory and presaged the idea of topology. The problem was to find a walk through the city that would cross each bridge once and only once. The islands could not be reached by any route other than the bridges, and every bridge must have been crossed completely every time (one could not walk half way onto the bridge and then turn around and later cross the other half from the other side). Euler proved that the problem has no solution.
At the mela, there was a 3d model of this problem, and students were trying to make a toy car travel through as many bridges as possible. The concept was then explained to them.
MathMagic
Pick a number between 1 and 60. There are five boards with random numbers in a grid. The “magician” will guess the number on your mind by checking if it appears on any of the boards. The number on your mind is the sum of the first numbers on all the boards that your number appears on.
Ames Room
An Ames room is a distorted room that is used to create an optical illusion. An Ames room is constructed so that from the front it appears to be an ordinary cubic-shaped room, with a back wall and two side walls parallel to each other and perpendicular to the horizontally level floor and ceiling. However, this is a trick of perspective and the true shape of the room is trapezoidal. As a result of the optical illusion, a person standing in one corner appears to the observer to be a giant, while a person standing in the other corner appears to be a dwarf. The illusion is convincing enough that a person walking back and forth from the left corner to the right corner appears to grow or shrink. This is used in television, special effects, etc.
At the mela, there was a 3D exhibit which children could learn this phenomen from. Through a peephole, they could see the optical illusion created.
Elliptical Carrom Board
With the striker and the other coin at the two focus points of the ellipse, when the striker is hit at any point of the circumference of the ellipse, it definitely passes through the second focus point, that is, hits the other coin.
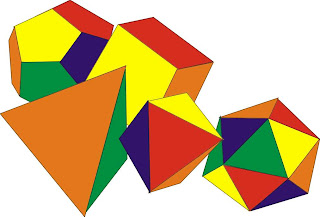
The 5 platonic solids
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and angles.
There are precisely five Platonic solids: Cube, Tetrahedron, Octahedron, Dodecahedron and Icosahedron
Playing with geometry, Constructions
Children played with straws, flat shapes, and blocks and built sculptures.
3D Animation
The origin of numbers, the 0, 1, the concept of binary numbers, the Fibonacci numbers, and the abacus.



No comments:
Post a Comment